what does it meqan for the roots of an equasion to be complex
| Encounter Quadratic Formula for a refresher on using the formula. In Algebra one, y'all institute that certain quadratic equations had negative foursquare roots in their solutions. Upon investigation, it was discovered that these square roots were chosen imaginary numbers and the roots were referred to equally complex roots. Permit's refresh these findings regarding quadratic equations and then expect a little deeper.
Consider this example:
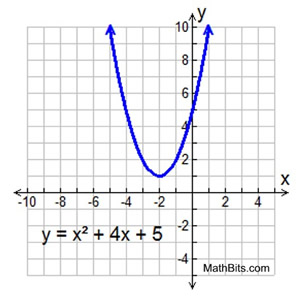
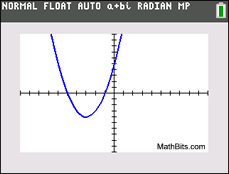
The circuitous roots in this example are x = -2 + i and x = -2 - i. These roots are identical except for the "sign" separating the two terms. One root is -2 PLUS i and the other root is -two MINUS i. Roots that possess this design are called circuitous conjugates (or cohabit pairs). This pattern of complex conjugates will occur in every set up of circuitous roots that you will run across when solving a quadratic equation. When expressed as factors and multiplied, these complex conjugates will permit for the middle terms containing "i "s to cancel out. If the roots of a quadratic equation are imaginary,
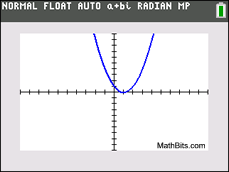
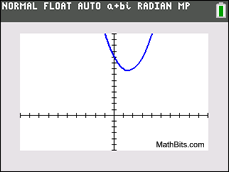
If the discriminant is negative, you have a negative under the radical The discriminant, b two - ivac , offers valuable data about the "nature" of the roots of a quadratic equation where a, b and c are rational values. It speedily tells you if the equation has 2 real roots (b two - 4ac > 0), i real repeated root (b 2 - 4air conditioning = 0) or two complex cohabit roots (b 2 - ivac < 0). If you are trying to determine the "blazon" of roots of a quadratic equation (not the actual roots themselves), you need not complete the entire quadratic formula. Simply wait at the discriminant.
Notation: The re-posting of materials (in function or whole) from this site to the Internet is copyright violation | ||||||||||||||||||||
Source: https://mathbitsnotebook.com/Algebra2/Quadratics/QDQuadratics.html
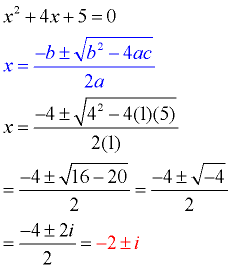
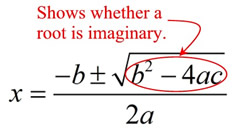
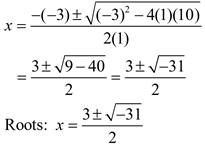

0 Response to "what does it meqan for the roots of an equasion to be complex"
Post a Comment